Vale a pena Ver!
sábado, 31 de agosto de 2013
Vale a pena ver!
Sonhe - Um dos melhores vídeos de inspiração para você agir
Nunca desista de seus sonhos!
Nunca desista de seus sonhos!
sexta-feira, 30 de agosto de 2013
Consequências!
Sem a Matemática não seria possível existir a Astronomia; sem os recursos prodigiosos da Astronomia seria impossível a Navegação. E a Navegação foi o fator máximo do progresso da Humanidade - Amoroso Costa.
Geometria Analítica - Vetores
Boa Tarde Pessoal!
➙ ➙ ➙
Escreva o vetor x em função dos vetores AB e AC,
➙
sabendo que P é o ponto médio de BC e M, N são
➙
pontos de trisecção do segmento AB.
➙ ➙ ➙
Temos x em função dos vetores AB e AC,
➙ ➙ ➙
ou seja, x = AB+ AC.
➙
Do vetor CB é dividido em duas partes e
➙
o vetor BA é dividido em três partes.
➙ ➙ ➙ ➙
A soma vetorial de x é: x = 1 PB + 2 BM
2 3
➙ ➙ ➙
PB é a metade do vetor CB, e BM é
➙
dois terços do vetor AB. Como nos mostra a figura abaixo:
➙ ➙ ➙ ➙
Substituindo PB por CB e BM por BA temos:
➙ ➙
x = 1 CB + 2 BA
2 3
➙ ➙
O exercício nos pediu x = AB+ AC
➙ ➙
e temos x = 1 CB + 2 BA,
2 3
➙
➙ ➙ ➙
Escreva o vetor x em função dos vetores AB e AC,
➙
sabendo que P é o ponto médio de BC e M, N são
➙
pontos de trisecção do segmento AB.
Temos x em função dos vetores AB e AC,
➙ ➙ ➙
ou seja, x = AB+ AC.
➙
Do vetor CB é dividido em duas partes e
➙
o vetor BA é dividido em três partes.
➙ ➙ ➙ ➙
A soma vetorial de x é: x = 1 PB + 2 BM
2 3
➙ ➙ ➙
PB é a metade do vetor CB, e BM é
➙
dois terços do vetor AB. Como nos mostra a figura abaixo:
➙ ➙ ➙ ➙
Substituindo PB por CB e BM por BA temos:
➙ ➙
x = 1 CB + 2 BA
2 3
➙ ➙
O exercício nos pediu x = AB+ AC
➙ ➙
e temos x = 1 CB + 2 BA,
2 3
➙
então teremos que fazer a soma vetorial de CB
➙
e inverter BA.
➙
Soma vetorial CB:
➙ ➙ ➙
CB = CA + AB
➙
Teremos que inverter o vetor CA, para ficar igual o
➙
que foi dado pelo exercício, então o vetor CA passa a
➙ ➙
ser AC e de positivo passa para negativo: - AC.
➙ ➙ ➙
CB = - AC + AB.
➙ ➙
Agora inverteremos 2 BA: - 2 AB.
3 3
Nunca se esqueçam de inverter o sinal quando for necessário a inversão do sentido do vetor.
➙
Iremos substituir a soma vetorial de CB na nossa
➙
equação e inverter o sentido do vetor AB
➙ ➙ ➙
CB = - AC + AB
➙ ➙
Então: x = 1 CB + 2 BA =
2 3
➙ ➙ ➙ ➙
x = 1 (-AC = AB) - 2 AB =
2 3
➙ ➙ ➙ ➙
x =- 1 AC + 1 AB - 2 AB
2 2 3
Agora devemos fazer a soma dos vetores iguais que aparecem mais de uma vez:
Irei fazer o calculo separado da equação:
➙ ➙
1 AB - 2 AB
2 3
m.m.c de 2 e 3 é 6 então temos:
➙ ➙ ➙
3AB - 4AB = - 1 AB
6 6
Chegamos ao último passo de nossa conta:
➙ ➙ ➙
x =- 1 AC - 1 AB
2 6
➙
e inverter BA.
➙
Soma vetorial CB:
➙ ➙ ➙
CB = CA + AB
➙
Teremos que inverter o vetor CA, para ficar igual o
➙
que foi dado pelo exercício, então o vetor CA passa a
➙ ➙
ser AC e de positivo passa para negativo: - AC.
➙ ➙ ➙
CB = - AC + AB.
➙ ➙
Agora inverteremos 2 BA: - 2 AB.
3 3
Nunca se esqueçam de inverter o sinal quando for necessário a inversão do sentido do vetor.
➙
Iremos substituir a soma vetorial de CB na nossa
➙
equação e inverter o sentido do vetor AB
➙ ➙ ➙
CB = - AC + AB
➙ ➙
Então: x = 1 CB + 2 BA =
2 3
➙ ➙ ➙ ➙
x = 1 (-AC = AB) - 2 AB =
2 3
➙ ➙ ➙ ➙
x =- 1 AC + 1 AB - 2 AB
2 2 3
Agora devemos fazer a soma dos vetores iguais que aparecem mais de uma vez:
Irei fazer o calculo separado da equação:
➙ ➙
1 AB - 2 AB
2 3
m.m.c de 2 e 3 é 6 então temos:
➙ ➙ ➙
3AB - 4AB = - 1 AB
6 6
Chegamos ao último passo de nossa conta:
➙ ➙ ➙
x =- 1 AC - 1 AB
2 6
Pessoal espero que tenham gostado e curtido, fiquem a vontade para deixar comentários e opiniões!
quinta-feira, 29 de agosto de 2013
Frações!
Boa Tarde Pessoal!
Para calcularmos adição e subtração de frações é utilizado o mesmo processo: Descobrir o mínimo múltiplo comum (m.m.c.), ou seja, o menor número que seja múltiplos dos dois denominadores.
2 + 5 =
6 2 ?????
Nossos denominadores são 6 e 2, então calculemos o m.m.c.
O menor número múltiplo de 6 e 2 é 2.Então:
Agora temos 3 e 1, e o múltiplo comum é 3. Então:
Portanto, nosso denominador é 6.
2 + 5 =
6 2 6
Vamos pegar o denominador que encontramos e dividi-lo pelo primeiro denominador, com o resultado multiplicamos numerador como mostrado abaixo:
A divisão do primeiro denominador deu 1 multiplicado por 2 que será 2.
A divisão do segundo denominador deu 3 multiplicado por 5 que será 15.
Então temos:
Multiplicação de frações
Na multiplicação de frações o sistema é mais simples, devemos apenas multiplicar numerador x numerador e denominador x denominador.
Divisão de frações
Na divisão de frações devemos conservar a primeira fração e inverter a segunda.
Agora mudemos o sinal de divisão pelo sinal de multiplicação e multiplicamos numerador x numerador e denominador x denominador.
Pessoal, espero que tenham gostado e curtido, fiquem a vontade para deixar comentários e opiniões!
Construção de Diagramas Cartesianos - Anamorfose.
Boa Noite Pessoal!
A energia potencial elástica de uma mola varia com a posição segundo a tabela anexa.
x(m)
|
0
|
0,10
|
0,20
|
0,30
|
0,40
|
0,50
|
0,60
|
0,70
|
EP
(J)
|
0
|
2,5
|
10
|
22,5
|
40
|
62,5
|
90
|
122,5
|
X²
(m²)
|
a) Construir o diagrama cartesiano (x;EP) e (x²;P) em papel milimetrado, indicando os módulos usados.
O papel milimetrado que iremos usar tem 13,5 cm no eixo x e 18 cm no eixo y.
Mx = ∆G --> m final - m inicial
∆L --> comprimento do papel no eixo x
Mx = ∆G = 0,70-0 = 0,058 m/cm
∆L 13,5
Iremos aproximar 0,05 m/cm para 0,1 m/cm, para facilitar a montagem do diagrama.
My = ∆G --> EP final - EP inicial
∆L --> comprimento do papel no eixo y
My = ∆G = 122,5-0 = 6,81 J
∆L 18 m
Iremos aproximar 6,81 J/cm para 10 J/m, para facilitar a montagem do diagrama.
Construindo o diagrama cartesiano:
x = para cada centímetro no eixo x de nosso papel milimetrado corresponderá a 0,1m.
Como o gráfico formou uma parábola, teremos que fazer Anamorfose, ou seja, elevar os valores do eixo x ao quadrado.
x(m)
|
0
|
0,10
|
0,20
|
0,30
|
0,40
|
0,50
|
0,60
|
0,70
|
X² (m²)
|
0
|
0,01
|
0,04
|
0,09
|
0,16
|
0,25
|
0,36
|
0,49
|
Mx = ∆G --> m² final - m² inicial
∆L --> comprimento do papel no eixo x
Mx = ∆G = 0,49-0 = 0,036 m/cm
∆L 13,5
Iremos aproximar 0,036 m/cm para 0,05 m/cm, para facilitar a montagem do diagrama.
EP
(J)
|
0
|
2,5
|
10
|
22,5
|
40
|
62,5
|
90
|
122,5
|
X² (m²)
|
0
|
0,01
|
0,04
|
0,09
|
0,16
|
0,25
|
0,36
|
0,49
|
Construindo o diagrama cartesiano:
x = para cada centímetro no eixo x de nosso papel milimetrado corresponderá a 0,05m.
b) Do gráfico (x²; EP) determinar a constante elástica da mola sabendo-se que EP = K.x²/2
Pegaremos dois pontos do plano cartesiano.
(x²)1; y1 (x²)2; y2
P1 = (0,04;10) e P2 = (0,36;90)
Iremos calcular o coeficiente angular que é a tangente do seu ângulo de inclinação.
b = ∆y --> y2 - y1 --> 90-10 --> 80 --> b = 250
∆x x2 - x1 0,36-0,04 0,32
Achamos o coeficiente angular (b), agora aplicamos a equação do 1º grau (EP = a+ b*(m²)) para encontrarmos o coeficiente linear da reta que é o ponto em que a reta corta o eixo y (eixo vertical).
Pegaremos um ponto qualquer do plano para efetuarmos o cálculo, P = (0,16;40)
Pegaremos um ponto qualquer do plano para efetuarmos o cálculo, P = (0,16;40)
EP = a + b*(m²)
40 = a + 0,16*250
a = 40 - 40
a = 0
Portanto a equação que relaciona t e v é: EP = 250*m²
EP = K*x²
2
250*x² = K* x²
2
2*250*x² = k*x²
500*x² = k*x²
500 = k*x²
x²
2
250*x² = K* x²
2
2*250*x² = k*x²
500*x² = k*x²
500 = k*
k = 500J/m²
Qualquer dúvida é só perguntarem nos comentários!
Pessoal, espero que tenham gostado e curtido, fiquem a vontade para deixar comentários e opiniões!
Derivadas!
Boa Noite Pessoal!
Hoje falarei um pouco sobre definição de derivadas e citarei um exemplo!
Bom, antes de mais nada, para que iremos usar derivadas?
Usamos derivada para calcular taxa de crescimento econômico do país, taxa de variação de temperaturas, taxa de crescimento de uma população, enfim, há inúmeros exemplos onde poderíamos aplicar uma função variante e qual a medida da variação em um determinado instante.
Vamos ver a definição da derivada de uma função em um determinado ponto.
A derivada de uma determinada função em um ponto x0 irá nos fornecer a taxa de variação instantânea de f em x0 e isto ocorre da seguinte maneira:
Uma determinada função y = f(x), onde x irá variar de x0 até x1, então iremos representar variação de x e y assim:
Em x: ∆x = x1 - x0.
Em y: ∆y = f(x1) - f(x0)
A figura a seguir ilustra a nossa situação:
Pessoal, espero que tenham gostado e curtido, fiquem a vontade para deixar comentários e opiniões!
Hoje falarei um pouco sobre definição de derivadas e citarei um exemplo!
Bom, antes de mais nada, para que iremos usar derivadas?
Usamos derivada para calcular taxa de crescimento econômico do país, taxa de variação de temperaturas, taxa de crescimento de uma população, enfim, há inúmeros exemplos onde poderíamos aplicar uma função variante e qual a medida da variação em um determinado instante.
Vamos ver a definição da derivada de uma função em um determinado ponto.
A derivada de uma determinada função em um ponto x0 irá nos fornecer a taxa de variação instantânea de f em x0 e isto ocorre da seguinte maneira:
Uma determinada função y = f(x), onde x irá variar de x0 até x1, então iremos representar variação de x e y assim:
Em x: ∆x = x1 - x0.
Em y: ∆y = f(x1) - f(x0)
A figura a seguir ilustra a nossa situação:
A nossa taxa média de variação de y por variação de x, no intervalo (x0,x1) será:
∆y = f(x1) - f(x0)
∆x x1 - x0
Onde:
f(x1) = (xo + ∆x)
x1 - x0 = ∆x
Portanto teremos:
∆y = f(x1) - f(x0) -------> ∆y = f(x0 +∆x ) - f(x0)
∆x x1 - x0 ∆x ∆x
Agora vamos aplicar o conceito no exemplo abaixo.
A posição de uma partícula em movimento sobre uma reta r é dada por m(t) = t² - 8t, onde m(t) é medida em metros e t em segundos.
a) Determinar a velocidade em um instante t = a qualquer.
Vm = m(a+ ∆t) - m(a)
∆t
Vm = ((a+∆t)² - 8(a + ∆t) - (a² -8a))
∆t
Vm = a² 2a∆t + ∆t² - 8a - 6∆t - a² + 8a
∆t²
Vm = 2a∆t + ∆t²- 8∆t
∆t²
Vm = 2a + ∆t- 8
Velocidade instantânea = lim (2a + ∆t- 6) --> 2a - 8
∆t → 0
b) Determinar a velocidade da partícula em t=0 e t=7.
t = 0 --> v(0) = 2*(0) - 8 --> -8 m/s
t = 7 --> v(0) = 2*(7) - 8 --> 6m/s
c) Determinar os intervalos de tempo durante os quais a partícula se move no sentido positivo e negativo sobre r.
Para m mover no sentido positivo terá que se mover para a direita, então temos:
2a - 8 > 0 --> a > 8/2 --> a > 4
t ϵ (-∞,4)
Para m mover no sentido negativo terá que se mover para a esquerda, então temos:
2a - 8 < 0 --> a < 8/2 --> a < 4
t ϵ (-∞,4)
d) Em que instante a velocidade é nula?
A velocidade será nula após 4 segundos.
V(a) = 0
2a - 8 = 0 --> a = 8/2 --> a = 4 s
Qualquer dúvidas é só perguntarem nos comentários!
Pessoal, espero que tenham gostado e curtido, fiquem a vontade para deixar comentários e opiniões!
quarta-feira, 28 de agosto de 2013
Construção de Diagramas Cartesianos
Boa Noite Pessoal
Mediu-se a velocidade de um móvel em vários instantes e obteve-se a tabela anexa:
T
(s)
|
0
|
20
|
40
|
60
|
80
|
100
|
V
(m/s)
|
60
|
120
|
180
|
240
|
300
|
360
|
a) Construir o diagrama cartesiano (t;v) em papel milimetrado, calculando os módulos utilizados.
O papel milimetrado que iremos usar tem 13,5 cm no eixo x e 18 cm no eixo y.
Pessoal prestem atenção nas medidas de cada papel milimetrado, pois dependendo a marca as medidas variam.
Pessoal prestem atenção nas medidas de cada papel milimetrado, pois dependendo a marca as medidas variam.
Mx = ∆G --> tempo final - tempo inicial
∆L --> comprimento do papel no eixo x
Mx = ∆G = 100-0 = 7,41 s/cm
∆L 13,5
Iremos aproximar o 7,41 s/cm para 10 s/cm, para facilitar a montagem do diagrama.
My = ∆G --> velocidade final - velocidade inicial
∆L --> comprimento do papel no eixo y
My = ∆G = 360-60 = 17,64 m/s
∆L 18 cm
Iremos aproximar o 17,64 (m/s)/cm para 20 (m/s)/cm, para facilitar a montagem do diagrama.
Construindo o diagrama cartesiano:
x = para cada centímetro no eixo x de nosso papel milimetrado corresponderá a 10s.
y = para cada centímetro no eixo y de nosso papel milimetrado corresponderá a 20 m/s.
b) Escrever a equação que relaciona t e v, sabendo que v= a + b.t
Pegaremos dois pontos do plano cartesiano.
x1; y1 x2; y2
P1 = (20;120) e P2 = (100;360)
Iremos calcular o coeficiente angular que é a tangente do seu ângulo de inclinação.
b = ∆y --> y2 - y1 --> 360-120 --> 240 --> b =3
∆x x2 - x1 100-20 80
Achamos o coeficiente angular (b), agora aplicamos a equação do 1º grau (v = a+ b*t) para encontrarmos o coeficiente linear da reta que é o ponto em que a reta corta o eixo y (eixo vertical).
Pegaremos um ponto qualquer do plano para efetuarmos o cálculo, P = ( 80; 300)
v = a + b*t
300 = a + 3*80
300 = a + 240
a = 300 - 240
a = 60
Portanto a equação que relaciona t e v é: v = 60 + 3*t
c) Para t = 50s quanto vale v?
v = 60 + 3*50
v = 210 m/s
Qualquer dúvidas é só perguntarem nos comentários!
Pessoal, espero que tenham gostado e curtido, fiquem a vontade para deixar comentários e opiniões!
terça-feira, 27 de agosto de 2013
A Grande Ciência!
" Tudo aquilo que as maiores inteligências, ao longo dos séculos, têm realizado em relação à compreensão das formas, por meio de conceitos preciosos, está reunido numa grande ciência: A Matemática." - J. M. Herbart.
Notação Científica!
Boa Noite Pessoal!
Bom ,hoje estava pensando em falar sobre como calcular log sem calculadora, mas antes irei explicar o conceito de notação científica, a qual usaremos nos cálculos de log.
Porque usarmos notação científica?
Bom, imaginemos um problema de física, a qual temos que representar a distância de Plutão ao Sol em centímetros, para representarmos todos os números dessa distância nos daria muito trabalho e ainda teríamos que contar todos os zeros tomando cuidado para não cometermos um equívoco, e consequentemente perderíamos alguns pontinhos na nossa nota da prova. hehe
Representação da Distância de Plutão ao Sol em cm: 590.000.000.000.000cm.
Ficou muito extenso e fácil de contarmos errados esta quantidade de zeros, agora vamos representá-lo em notação científica: 5,9*1014.
Acredito que não seja necessário contestar a importância da notação científica após esta simples apresentação.
Aprendendo a colocar em notação científica
Para colocarmos números muito extensos em notação científica, é só contarmos as casas decimais da direita para a esquerda até chegarmos na primeira casa decimal.
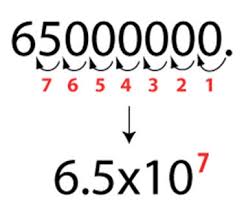Exemplo: 723.000.000 = 7,23 x 108
Para facilitar na contagem irei colocar vírgulas na cor vermelha representando cada casa decimal:
7,2,3,0,0,0,0,0,0 = 7,23 x 108
Agora para colocarmos números menores que 1 em notação científica, é só contarmos as casas decimais da esquerda para a direita até chegarmos na última casa decimal.
Exemplo: 0,000 000 098 = 9,8 x 10-8
Para facilitar na contagem irei colocar vírgulas na cor vermelha representando cada casa decimal:
0,0,0,0,0,0,0,9,8 = 9,8 x 10-8
Um pouco de teoria!!!!
Apresentarei a vocês algumas regras básicas:
"a" é a nossa base e "b" é o nosso expoente, então temos: ab
1ª Regra: na multiplicação deve-se conservar a base e somar os expoentes:
25 x 22 = 27
3ª Regra: para passarmos o denominador para o numerador, basta apenas invertermos o sinal do expoente.
2 = 2 x 10 -2
Bom ,hoje estava pensando em falar sobre como calcular log sem calculadora, mas antes irei explicar o conceito de notação científica, a qual usaremos nos cálculos de log.
Porque usarmos notação científica?
Bom, imaginemos um problema de física, a qual temos que representar a distância de Plutão ao Sol em centímetros, para representarmos todos os números dessa distância nos daria muito trabalho e ainda teríamos que contar todos os zeros tomando cuidado para não cometermos um equívoco, e consequentemente perderíamos alguns pontinhos na nossa nota da prova. heheRepresentação da Distância de Plutão ao Sol em cm: 590.000.000.000.000cm.
Ficou muito extenso e fácil de contarmos errados esta quantidade de zeros, agora vamos representá-lo em notação científica: 5,9*1014.
Acredito que não seja necessário contestar a importância da notação científica após esta simples apresentação.
Aprendendo a colocar em notação científica
Para colocarmos números muito extensos em notação científica, é só contarmos as casas decimais da direita para a esquerda até chegarmos na primeira casa decimal.
Para facilitar na contagem irei colocar vírgulas na cor vermelha representando cada casa decimal:
7,2,3,0,0,0,0,0,0 = 7,23 x 108
Agora para colocarmos números menores que 1 em notação científica, é só contarmos as casas decimais da esquerda para a direita até chegarmos na última casa decimal.
Exemplo: 0,000 000 098 = 9,8 x 10-8
Para facilitar na contagem irei colocar vírgulas na cor vermelha representando cada casa decimal:
0,0,0,0,0,0,0,9,8 = 9,8 x 10-8
Um pouco de teoria!!!!
Apresentarei a vocês algumas regras básicas:
"a" é a nossa base e "b" é o nosso expoente, então temos: ab
1ª Regra: na multiplicação deve-se conservar a base e somar os expoentes:
25 x 22 = 27
2ª Regra: na divisão deve-se conservar a base e subtrair os expoentes:
25 = 25-2= 23
25 = 25-2= 23
3ª Regra: para passarmos o denominador para o numerador, basta apenas invertermos o sinal do expoente.
2 = 2 x 10 -2
10 2
Pessoal, espero que tenham gostado e curtido, , fiquem a vontade para deixar comentários e opiniões!
Pessoal, espero que tenham gostado e curtido, , fiquem a vontade para deixar comentários e opiniões!
Assinar:
Postagens (Atom)
