Num corpo de massa 2 kg atuam as forças F e de atrito cinético fatc, conforme mostra a figura.. Essas forças são paralelas ao deslocamento que ocorre no plano horizontal. No instante t=0, o corpo se encontra na origem dos espaços (S0=0) e em repouso (vo=0).
Calcule:
a) o trabalho realizado por F ao longo de 6m;
Para determinar-se o trabalho realizado por F ao longo de 6m, deve-se calcular a área de cada figura geométrica apresentada no gráfico.
Área do Quadrado: b.h
2.10 = 20J
Área do trapézio: (b+B).h
2
(10 + 20).2 = 30J
2
Área do triângulo: b.h
2
2.20 = 20J
2
Somatória dos trabalhos realizados:
τ0-6 = 20 + 30+ 20
τ0-6 = 70J
b) o trabalho da força de atrito ao longo de 6m;
Para determinar-se o trabalho realizado da força de atrito ao longo de 6m, deve-se calcular a área do retângulo correspondente a Força fat.
Área do Retângulo: b.h
-9 . 6 = -54J
-9 . 6 = -54J
c) o trabalho da força resultante que atua no corpo ao longo dos 6m;
Para determinar-se o trabalho da força resultante que atua no corpo ao longo de 6m, deve-se calcular todas as forças atuante no corpo de massa 2kg.
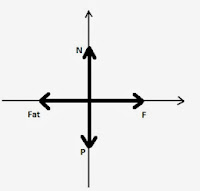
No bloco há as seguintes forças: Normal, Peso, Força e Fat.
Ao analisar o diagrama nota-se que as forças Normal e Peso formam angulação de 90 graus com o eixo x, sabe-se que cos 90 = 0, portanto as forças Normal e Peso será zero, isto nos privará de realizar contas e perder tempo desnecessário:
F e Fat já havia sido calculado portanto basta realizar a somatória do trabalho da força resultante que atua no corpo ao longo dos 6m.
Frτ0-6 =
Fτ0-6 + Pτ0-6 + Nτ0-6+
Fatτ0-6
Frτ0-6 = 70 + 0 + 0 - 54
Frτ0-6 = 16J
d) a velocidade do móvel na posição 6m.
Frτ0-6 = Еcf - Еci
Sabe-se que a energia cinética inicial é nula, pois a velocidade neste instante será 0.
Frτ0-6 = Еcf
Frτ0-6 = m.v²
2
16 = 2. v²
2
v² = 16
v = √16
v = 4 m/s
Pessoal, se tiverem alguma dúvida ou se não entenderam alguma coisa, é só perguntar nos comentários. Espero que tenham gostado e curtido!


Nenhum comentário:
Postar um comentário