Análise Dimensional e Adimensional II

Um manual mostra que a gravação de um microchip segue aproximadamente a relação:

d = 16,2 - 16,2e^-0,021.t, onde:

d = profundidade da gravação (µm)

t = tempo da gravação (s)

Quais são as unidades associadas aos números 16,2 e 0,021? Converta a relação de forma que d seja expresso em polegadas e t em minutos.

As unidades associadas aos números 16,2 e 0,021 é micrometro (µm) e segundos (s) respectivamente.

Simplificando a equação temos:

d = 16,2 - 16,2e^-0,021.t

d = 16,2.(1 - e^-0,021.t)

Convertendo 16,2 µm para in:

16,2µm  .      1m          .  39,37 in  = 6,4 . 10^-4 in

                  10^6µm           1m     

- 0,021.t = - 0,021.  1   .  60 s  =-1,26    1   

                                s      1min             min

Então:

d = 6,4 . 10^-4.(1 - e^-.t)

Considere a seguinte expressão µ = c. √ΔP / P, onde:

µ = velocidade do fluido

ΔP = queda da pressão

p = densidade do fluido

c = constante

Qual é a unidade de c no sistema de unidade SI?

Sabe-que:

µ = m/s 

ΔP = P = F/A

F = m.a

P =    Kg. m   

         m² . s²

P =   kg   

        m.s²

p =     Kg   

          m³

µ = c. √ΔP / P

   m    = c.√(Kg)/m.s²

   s               (Kg)/m³

Calculando o que está na raiz

 =       Kg   

        m.s²       

         Kg  

        m³

=    Kg   .    m³  

      m.s²     Kg

=    m²   

       s²

Então:

   m    = c.√  m²   

    s               s²

   m    = c.  m   

    s             s

c = (m/s) / (m/s)

c = 1

C é adimensional 

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Análise Dimensional e Adimensional

Qual é a dimensão de K na seguinte equação: K = (1/2) mv²

Sabe-se que:
m = M 

v = L.T-1

(1/2) = é um fator puramente numérico, portanto é igual a um, isto é,  = M⁰L⁰T<sup>0 = 1

K = M.(L.T^-1)</sup>²

K = M.L²T-1

Determine inteiros b,c e d diferentes de zero tais que a^bv^ct^d

seja adimensional:

Sabe-se que:

a = m/s²
v = m/s
t = s 

a^bv^ct<sup>d

   m    .    m    . s</sup>
  s²        s

Observando a equação, nota-se que será impossível b,c e d serem adimensionais pois tem-se    m².s  , para que possam  
                                               s³
ser adimensionais inverter-se-a a unidade da velocidade:

a^bv^ct<sup>d

   m    .    m    . s</sup>
  s²        s

   ^{m    . (m/s)^-1 . s}
  s²        

   ^{m    .    (m^-1)} . s
  s²       (s^-1)

   ^{m    .    s    . s}
  s²       m

   m.s²  
  s².m


Pessoal espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Análise dimensional - Verificação de validade de equações

Seja a equação x = xo + vt 0,5at³ onde x representa um comprimento, t um tempo, v uma velocidade e a uma aceleração. Por meio da análise dimensional, verifique a validade desta equação.

Sabe-se que a unidade de comprimento é em "m", velocidade em "m/s, de tempo é em "s" e a aceleração em m/s², portanto tem-se:

x = xo + vt+ 0,5at³

m = m +    m   .s +    m    . s³

                 s               s²

m = m +    m   .  s +    m    . s³ 

                 s               s²

m = m + m + m.s

Não é válida pois m ≠ m 

Seja a equação x = xo + 0,5at² onde x representa um comprimento, t um tempo, v uma velocidade e a uma aceleração. Por meio da análise dimensional, verifique a validade desta equação.

Sabe-se que a unidade de comprimento é em "m", velocidade em "m/s, de tempo é em "s" e a aceleração em m/s², portanto tem-se:

x = xo + vt+ 0,5at³

m = m +    m   .s +    m    . s²

                 s               s²

m = m +    m   .  s +    m    . s² 

                 s               s²

m = m + m + m

A equação é válida pois m = m 

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Análise Dimensional - Conversão de Unidades

Para resolução dos problemas faremos uma abordagem em que as unidades são tratadas como quantidades algébricas. Esta técnica é chamada de Análise Dimensional.

O elemento chave na utilização da análise dimensional é o correto uso dos fatores de conversão de uma unidade para outra. Um fator de conversão é uma fração cujo numerador e o denominador são as mesmas grandezas em unidades diferentes.

Então: 

Unidade dada .  Unidade Desejada  = Unidade Desejada

                           Unidade Dada

Exemplo 1: Converta:

a) O comprimento em Km de 500 mi é?

Sabe-se que 1 mi = 1,609 Km portanto tem-se:

Unidade dada .    Unidade Desejada     = Unidade Desejada

                            Unidade Dada

500 mi .    1,609 Km    = 804,5 Km

                    1 mi

Exemplo 2: Quanto equivale 65 milhas por horas em?

a) ft/s:

Sabe-se que:

1 mi = 1,609 km

1km = 10³m

1m = 3,28084 ft

1h = 3600s

65mi  . 1,609km  .  10³ m  .  3,28084ft ft  .    1h    = 95,31 ft/s 

   1h       1mi          1Km           1 m           3600 s 

b) cm/s:

Sabe-se que:

1km = 0,6214mi

1km = 10^5 cm

1h = 3600s

65mi  .      1km          .  10^5 cm  .     1h    = 2905,62 cm/s

   1h       0,6214mi           1Km       3600 s 

Exemplo 3: A velocidade  da luz no vácuo é 3,00  x 10^8 m/s. Converta esta velocidade em milhas por segundo.

Sabe-se que:

1km = 1000m

1km = 0,6214 mi

3,00.10^8m  .      1km          .  0,6214mi  = 1,86 . 10^5 m/s

   1 s                 1000 m           1Km     

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Cinemática dos Sólidos V

Uma pedra de esmeril de formato cilíndrico, com raio R=0,45m, gira com frequência constante fo=1800 r.p.m.; quando se desliga o motor elétrico do esmeril, a pedra gasta 10s até parar; considerando o movimento uniformemente acelerado, pedem-se:

a) A aceleração angular (alfa) da pedra; 

A roda gira com frequência constante de 1800 r.p.m.

ωa =    2πf   
            60

ωa =    2π.1800   

             60

ωa = 188,49 rad/ s

Sabe-se que a velocidade final é 0, portanto tem-se:

ω = ωo + α.t 

0= 188,49 + 10.α

α =    -188,49   

         10

α = -18,85 rad/s²

b) A velocidade de um ponto P da borda da pedra, quando a frequência é f = 1800 r.p.m ; 

Para determinar-se a velocidade em um ponto P na periferia, sabe-se que Vp = ωa.R:

Vp = ωa.R

Vp = 188,9x0,45

Vp = 84,82 m/s

c) A aceleração de um ponto P da borda da pedra, quando a frequência é f=180 RPM

A aceleração possui 2 componentes: a aceleração tangencial e a normal:

αtangencial= α. R 

αnormal= ω . V

Neste caso usaremos aceleração normal:

αnormal= ω . V

αn= 84,82.188,49

αn= 15987,72 m/s²

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Cinemática dos Sólidos IV

O disco de raio R=80mm parte do repuso e acelera de forma uniforme, atingindo a velocidade angular w= 30 rad/s em 10 voltas. Pedem-se:

 a) A aceleração angular do disco

Antes de aplicar a equação de Torricelli, observa-se que não temos o deslocamento da disco, portanto com as informações do número de voltas do disco calcula-se o deslocamento.

Δθ = 10.2π

Δθ = 20π rad

Aplicando equação de Torricelli:

ω² = ωo² + 2α.Δθ

30² = 0² +  2α.20π

   900    = α

   40π

α = 7,16 rad/s²

 b) O tempo gasto nessas 10 voltas.

ω = ωo + α.t 

30= 0 + 7,16.t

t =    30   

       7,16

t = 4,19s

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Calorimetria VI

Num calorímetro de capacidade térmica 8 cal/ºC inicialmente a 10ºC são colocados 200g de um líquido de calor específico 0,40 cal/gºC. Verifica-se que o equilíbrio térmico se estabelece a 50ºC. Determine a temperatura inicial do líquido.

1º Sistema: O calorímetro está com temperatura inicial de 10ºC, em seguida adiciona um líquido cuja temperatura inicial deseja-se descobrir, o equilíbrio térmico estabelecido é de 50ºC.

Qcalorímetro + Qlíquido  = 0

Cc.ΔTc + ml.Cl.ΔTl  = 0

8.(50 - 10) + 200.0,40.(50 -T1) = 0

320 + 80.(50 - T1) = 0

320 + 4000 - 80.T1 = 0 = 0

80.T1 = 4320

T1 = 4320/80

T1 = 54ºC

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Calorimetria V

Um corpo de massa 100g que está a uma temperatura de 238ºC é colocado no interior de 200g de água a 20ºC. Após atingir o equilíbrio térmico, a 38ºC, o corpo é retirado e introduzido no interior de 100g de água a 62ºC. Desprezando as eventuais perdas de calor e sabendo que o calor específico da água é 1,0cal/g.°C, determine a temperatura final de equilíbrio térmico.

1º Sistema: O corpo está com temperatura inicial é de 238ºC, ao ser colocado em um recipiente contendo água cuja temperatura é de 20ºC - temperatura inicial  referente à água -, deseja-se resfriar o sistema para 38ºC - temperatura final referente à todo o sistema - para determinar o calor específico do corpo.

Qcorpo + Qágua  = 0

mc.Cc.ΔTc + ma.Ca.ΔTa  = 0

 100.C.(38 - 238) + 200.1.(38 - 20) = 0

-20000 + 3600.C = 0

C = -20000/3600

Cal= 0,18 cal/gºC

2º Sistema: O corpo cuja temperatura após sair do primeiro sistema é de 38ºC é colocado em um recipiente de água de 62ºC, determinar o calor final do processo.

Qcorpo + Qágua  = 0

mc.Cc.ΔTc + ma.Ca.ΔTa  = 0

 100.0,18.(T - 38) + 100.1.(T -62) = 0

18T - 684 + 100T - 6200 = 0

118T - 6884 = 0

T = -6884/118

T = 58,34ºC

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Calorimetria IV

Quando 500g de chumbo (c = 0,02cal/g.ºC) a 100ºC são colocados em um calorímetro de alumínio (c = 0,2cal/g.ºC) de massa 100g e que contém 300g de azeite de oliva a 20ºC, a temperatura final da mistura é 30ºC. Determine o calor específico do azeite, em cal/g.ºC.

No sistema do calorímetro e do azeite a temperatura inicial é de 20ºC, ao acrescentar chumbo cuja temperatura é de 100ºC - temperatura inicial  referente ao chumbo -, deseja-se resfriar o sistema para 30ºC - temperatura final referente à todo o sistema.

Qcalorímetro + Qchumbo + Qazeite = 0

Mc.Cc.ΔTc + mch.Cch.ΔTch = ma.Ca.ΔTa = 0

100.0,2.(30 - 20) + 500.0,02.(30 - 100) + 300.Ca.(30 - 20) = 0

200 -700 + 3000.Ca = 0

3000Ca = 500

Ca = 500/3000

Ca = 0,16 cal/gºC

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Calorimetria III

Um calorímetro, de capacidade térmica desprezível, contém 100g de água a 15,0°C. Adiciona-se no interior do calorímetro uma peça de metal de 200g, à temperatura de 95,0°C. Verifica-se que a temperatura final de equilíbrio é de 20,0°C. Qual o calor específico do metal, em cal/g.°C?

A água está com temperatura inicial é de 15ºC, ao acrescentar a peça metálica cuja temperatura é de 95ºC - temperatura inicial  referente à peça metálica -, deseja-se resfriar o sistema para 20ºC - temperatura final referente à todo o sistema.

 Qágua + Qmetal  = 0

mag.Cag.ΔTag + mm.Cm.ΔTm   = 0

 100.1.(20 - 15) + 200.C.(20 - 95) = 0

500 - 1500.C = 0

C = 500/1500

mal = 0,033 cal/gºC

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Calorimetria II

Uma senhora diz à sua filha de 10 anos para encher uma bacia com água e álcool, para que possa fazer uma massagem em seus pés. A criança coloca 0,3L de água a 80°C (apenas água quente) na bacia. Calcule a quantidade de álcool a 20°C necessária para baixar a temperatura da mistura na bacia para 50°C. Desconsidere a capacidade térmica da banheira.

(Dados: cálcool = 0,2 cal/gºC; 1L de água equivale a 1kg de massa.)

A água está com temperatura inicial é de 80ºC, ao acrescentar o álcool cuja temperatura é de 20ºC - temperatura inicial  referente ao álcool -, deseja-se resfriar o sistema para 50ºC - temperatura final referente à todo o sistema.

 Qágua + Qálcool  = 0

mag.Cag.ΔTag + mal.Cal.ΔTal   = 0

 300.1.(50 - 80) + mal.0,2.(50 - 20) = 0

-9000 + 6.mal = 0

mal = -9000/6

mal = 1500g

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Calorimetria I

Um calorímetro contém 200g de água, e o conjunto está à temperatura de 20ºC. Ao ser acrescentado ao calorímetro 125g de uma liga metálica a 130ºC, verificamos que após o equilíbrio térmico a temperatura final do sistema é de 30ºC. Qual é a capacidade térmica do calorímetro? (Dados: calor específico da liga = 0,20 cal/g.ºC)

Obs: Massa do calorímetro é desprezível.

 No sistema do calorímetro e da água a temperatura inicial é de 20ºC, ao acrescentar uma liga cuja temperatura é de 130ºC - temperatura inicial  referente à liga -, deseja-se resfriar o sistema para 30ºC - temperatura final referente à todo o sistema.

Qcalorímetro + Qágua + Qliga = 0

Cc . ΔTc + ma . Ca . ΔTa = ml . Cl . ΔTl = 0

Cc.(30 - 20) + 200.1.(30 - 20) + 125.0, 2.(30 - 130) = 0

Cc.10 + 2000 - 2500 = 0

10.Cc = 500

Cc = 50 cal/gºC

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Cinemática dos Sólidos III

A polia ilustrada, possui raio R=0,32m e é acionada por um motor elétrico, com o intuito de suspender o bloco A. quando a polia apresenta frequência de rotação fo=120 r.p.m., o motor é desligado, mesmo assim, o bloco ainda sobe h= 0,8 m antes de parar. pedem-se: 

a) a aceleração angular da polia; 

A roda gira com frequência constante de 120 r.p.m.

ωa = 2πf

ωa = 2π.120

ωa = 753,98 rad/ min

Não olvidar de converter minutos para segundos, pois sempre se trabalhará com segundos

   753,98   = 12,56 rad/s

   60

Antes de aplicar a equação de Torricelli, observa-se que não temos o deslocamento da polia, portanto com as informações da altura e do raio da polia calcula-se o deslocamento.

Δθ = S/R

Δθ = 0,8/0,32

Δθ = 2,5m

Aplicando equação de Torricelli:

ω² = ωo² + 2α.Δθ

0 = 12,56² + 2α.2,5

   -157,75    = α

       5

α = - 31,55 rad/s²

b) o tempo gasto até parar.

Aplicando a equação da velocidade, temos:

ω = ωo + α.t 

0= 12,56 + (-31,55).t

t =    -12,56   

       -31,55

t = 0,39s

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!

Cinemática dos Sólidos II

O sistema ilustrado, composto por uma placa de dimensões 0,20 x 0,40 soldada ao eixo fixo AB,  gira em torno deste, com velocidade angular 15 rad/s, que decresce a taxa de 7 rad/s2.  Quando observada do ponto B, a placa gira no sentido anti-horário.

Para o instante ilustrado,  Pedem-se:

a) a velocidade do ponto C

- A direção é a do eixo definida pelos pontos A e B;

- O sentido é dado pela regra da mão direita;

- Para determinar-se a velocidade do ponto C deve-se aplicar a fórmula seguinte:

→

ω = ω.ê

Onde ê é dada pela fórmula:

ê =    (A-B)   

         ||A-B||

Coordenadas dos pontos de interesse 

Calculando o vetor de (A-B)

(A-B) = (0,40-0).î + (-0,10-0,10).ǰ +  (0,20-0).ǩ

(A-B) = 0,40.î -0,20.ǰ + 0,20.ǩ

Calculando o versor de ||A-B||

 ||A-B|| = √ 0,40² -0,20² + 0,20²

 ||A-B|| = √ 0,16 + 0,04 + 0,04

 ||A-B|| = √ 0,24

 ||A-B|| = 0,49

Calculando ê:

ê =    (A-B)   

         ||A-B||

ê =     0,40.î -0,20.ǰ + 0,20.ǩ     

                     0,49

ê = 0,82.î -0,41.ǰ + 0,41.ǩ

Calculando ω:

Sabe-se que a velocidade angular dada pelo exercício é de 15 rad/s.

→

ω = ω.ê

→

ω = 15. (0,82.î -0,41.ǰ + 0,41.ǩ)

→

ω = 12,2.î - 6,1.ǰ + 6,1.ǩ

Determinando Velocidade do Ponto C

  

   →

Vc = ω ^(C-A)

Determinando C-A

(C-A) = (0,40-0).î + (0-0,10).ǰ +  (0,20-0).ǩ

(C-A) = 0,40.î -0,10.ǰ + 0,20.ǩ

   →

Vc = ω ^(C-A)

Vc = (12,2.î - 6,1.ǰ + 6,1.ǩ) ^ (0,40.î -0,10.ǰ + 0,20.ǩ)

Determinando Velocidade eixo x:

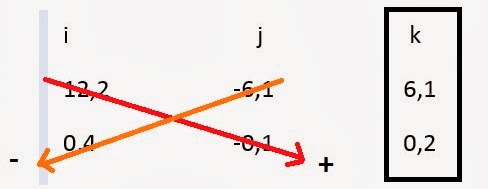
Sabe-se que x = i, portanto para calcular-se a velocidade em x, deve-se isolar a coluna i e multiplicar em cruz, como mostra a figura abaixo:

Obs: Sentido esquerda para direita (flecha vermelha) é positiva e sentido direita para esquerda (flecha laranja) é negativa.

Vx = [(-6,1).0,2] - [(-0,1).6,1]

Vx = -1,22 + 0,61  

Vx = -0,61

Determinando Velocidade eixo y:

Sabe-se que y = j, portanto para calcular-se a velocidade em y, deve-se isolar a coluna j e multiplicar em cruz, como mostra a figura abaixo:

Vy = - (12,2.0,2) - ( 0,4.6,1)

Vy = -(2,44 - 2,44)  

Vy = 0

Determinando Velocidade eixo z:

Sabe-se que z = k, portanto para calcular-se a velocidade em z, deve-se isolar a coluna k e multiplicar em cruz, como mostra a figura abaixo:

Vz = [12,2.(-0,1)] - [0,4.(-6,1)]

Vz = -1,22 + 2,44  

Vz = 1,22

Somando as velocidades de cada eixo, temos:

Vc = -0,61.î + 1,22.ǩ

b) a aceleração do ponto C

Para aceleração do ponto C tem-se:

α = ω.ê

Na alternativa A já foi calculado ê, portanto privemo-nos de cálculos, deixarei apenas o resultado, e, sabe-se que há uma taxa decrescente de 7 rad/s², portanto se decresce seu valor será negativo.

 α = -7.(0,82.î -0,41.ǰ + 0,41.ǩ)

 α = -5,74.î + 2,87.ǰ - 2,87.ǩ rad/s²

Não olvidem-se de calcular o vetor aceleração do ponto C

→  →             →       →

ac = α ^(C-A) + ω ^ [ ω ^(C-A)]

Calcular-se-á por partes para melhor entendimento do exercício.

α = (-5,74.î + 2,87.ǰ - 2,87.ǩ)

(C-A) = (0,40.î -0,10.ǰ + 0,20.ǩ)

→        

 α ^(C-A)

(-5,74.î + 2,87.ǰ - 2,87.ǩ) ^  (0,40.î -0,10.ǰ + 0,20.ǩ)

Determinando aceleração eixo x:

Vx = (2,87.0,20) - [(-2,87).(-0,10)]

Vx = 0,574 - 0,087  

Vx = 0,487

Determinando aceleração eixo y:

Vy = - (5,74.0,20) - [(-2,87).0,40]

Vy = -(1,148 + 1,148)  

Vy = -2,296

Determinando aceleração eixo z:

Vz = [5,74(-0,10)] - (2,87.0,40)

Vz = -0,574 - 1,148

Vz = - 1,722

Somando as velocidades de cada eixo, temos:

 →        

 α ^(C-A) = 0,487.î -2,296.ǰ - 1,722.ǩ

Não olvidem-se de calcular o vetor velocidade do ponto C

→  →             →       →

ac = α ^(C-A) + ω ^ [ ω ^(C-A)]

Calcular-se-á por partes para melhor entendimento do exercício.

→

ω = 12,2.î - 6,1.ǰ + 6,1.ǩ

[ ω ^(C-A)] = -0,61.î + 1,22.ǩ

→    →

 ω ^ [ ω ^(C-A)] = (12,2.î - 6,1.ǰ + 6,1.ǩ) ^  (-0,61.î + 1,22.ǩ)

Determinando velocidade eixo x:

Vx = [(-6,1).1,23) - (6,1.0,0)

Vx = -7,5 - 0

Vx = -7,5

Determinando aceleração eixo y:

Vy = - (12,2.1,23) - [(-0,61).6,1]

Vy = -(15,006 + 3,721)  

Vy = -18,727

Determinando aceleração eixo z:

Vz = (12,2.0,00) - [(-0,61).(-6,1)]

Vz = 0 - 3,721

Vz = - 3,721

Somando as velocidades de cada eixo, temos:

→    →

 ω ^ [ ω ^(C-A)] = -7,5.î -18,727.ǰ - 3,721.ǩ

Finalizando os cálculos

→  →             →       →

ac = α ^(C-A) + ω ^ [ ω ^(C-A)]

→

ac = (0,487.î -2,296.ǰ - 1,722.ǩ) + (-7,5.î -18,727.ǰ - 3,721.ǩ)

→

ac = -7,01.î -21,02.ǰ+ 5,44.ǩ

Pessoal, espero que tenham gostado e curtido,  fiquem a vontade para deixar comentários e opiniões!