₵υℓƭυπα ƐχαtαƧ: Área de uma figura Geométrica

Boa tarde Pessoal!

Área das figuras geométricas

Quadrado

O quadrado possui todos os lados iguais, seus ângulos internos são iguais (90º) e suas diagonais são perpendiculares.

A = LxL ou A = L²

Exemplo:

1) Um quadrado tem 9m de lado, qual a sua área?

A = 9x9 → A = 81m
ou
A = 9² → A = 81m²

2) Um quadrado tem área de 225m², qual a medida de cada lado?
Área do quadrado = 225m²
lado = ??

225 = L² → L = √225 → L = 15m²

Todo quadrado é um losango, mas nem todo losango é um quadrado, da mesma forma que todo quadrado é um retângulo, mas nem todo retângulo é um quadrado.

Retângulo

Os retângulos são quadrilátero equiângulo, ou seja todos seus ângulos internos são iguais e os lados opostos também são iguais.

A área do retângulo é A = a x b

Diego comprou um terreno cujas dimensões são: 12 metros de largura e 40 metros de comprimento. Qual será a área do terreno?
a = 12 metros
b = 40 metros

A = a x b
A = 12 x 40 → A = 480 m²

Triângulo Retângulo

O triângulo retângulo apresenta um ângulo reto e dois ângulos agudos. A soma desses Ângulos deve dar 180º, o ângulo reto é de 90º e o dos ângulos agudos podem variar desde que a soma dos três ângulos seja igual a 180º.

Exemplo: O triângulo retângulo abaixo apresenta ângulo reto de 90º e dois ângulos agudos de 60º e 30º, perfazendo somatória de 180º.

A área do triângulo retângulo é dada pela fórmula:

A = b x a
2

Exemplo:
Um triângulo apresenta 4m de base e 7m de altura, qual a área do triângulo?
b = 4m
a = 7m

A = 4 x 7 → A = 28 → A = 14m²

2 2

Triângulo Acutângulo
Um triângulo acutângulo apresenta todos os ângulos agudos, ou seja, menor que 90º e maior que 0º.

A área do triângulo retângulo é dada pela fórmula:

A = c x h
2

Triângulo Obtusângulo

Um triângulo obtusângulo é um triângulo que possui um dos ângulos obtuso, ou seja, maior que 90º e menor que 180º.

A área do triângulo retângulo é dada pela fórmula:

A = c x h
2

Triângulo Equilátero

O triângulo equilátero possui ângulos internos congruentes e medem 60º

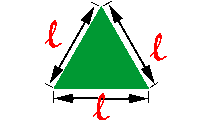
A área do triângulo equilátero é dada pela fórmula:

A = L² √3
4

Exemplo:
1) Qual a área de um triângulo equilátero cujo lados medem 7mm.

A = 7² √3 → A = 49 √3 → A = 12,25√3 → A = 21,21mm²
4 4

Losango

Suas diagonais são perpendiculares, e assim como o paralelogramo, o losango apresenta os lados e ângulos opostos congruentes, ou seja, possui o mesmo tamanho e o mesmo ângulo respectivamente.

A área do losango é dada pela fórmula:

A = D x d
2

Exemplo:

1) Qual a área de um losango cuja diagonais medem 7m e 18m?

d = 7m

D = 18m

A = ?

A = 18 x 7 → A = 126 → A = 63m²
2 2

Paralelogramo

Os lados e ângulos opostos do paralelogramo são congruentes, ou seja, possui o mesmo tamanho e o mesmo ângulo respectivamente.

A área do paralelogramo é dada pela fórmula:

A = a x b

Exemplo:

1) Um paralelogramo apresenta 10 cm de altura e 13 cm de base, qual é a área desse paralelogramo?

A = 10 x 13 → A = 130 cm²

Trapézio

O Trapézio possui duas bases paralelas B e b, e em um trapézio retângulo tem um dos lados perpendicular às bases formando assim ângulo de 90º.

A área do trapézio é dada pela fórmula:

A = (B + b) x h

Pentágono

Para calcularmos a área do pentágono, basta dividirmos em cinco triângulo equilátero, achar a área do triângulo equilátero e multiplicarmos por 5, que é a quantidade de triângulos equiláteros que compõe um pentágono.

A área do pentágono é dada pela fórmula:

A =5x L² √3
4

Hexágono Regular
Para calcularmos a área do hexágono, basta dividirmos em seis triângulo equilátero, achar a área do triângulo equilátero e multiplicarmos por 6, que é a quantidade de triângulos equiláteros que compõe a área de um hexágono.

A área do hexágono regular é dada pela fórmula:

A = 6 x L² √3
4

Círculo
Círculo é denominado como conjunto dos pontos internos de uma circunferência.

A área do trapézio é dada pela fórmula:

A =R² x π

Coroa Circular

Coroa circular é a região limitada por dois círculos concêntricos, onde R é o raio do círculo maior e r é o raio do círculo menor.

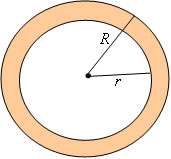
A área da coroa circular é dada pela fórmula:

A = πR² - πr²

Setor Circular

Setor Circular é a parte de um círculo limitado por dois raios e um arco.